2. 가우스 소거법을 이용한 연립방정식의 풀이

1. 가우스 소거법 : [2 x 2] 행렬

가우스 소거법(Gaussian Elimination)은 연립방정식의 해를 구하기 위한 체계적인 알고리즘입니다. 직관적이고 간단한 원리를 가지고 있을 뿐 아니라, 행렬에 대한 유용한 정보를 다수 도출할 수 있기 때문에 많은 소프트웨어가 행렬 연산을 수행할 때 자주 사용하는 알고리즘이기도 합니다.

가우스 소거법이라는 이름은 익숙하지 않을 수 있지만, 이미 많은 분들이 이 방법을 이용하여 자연스럽게 연립방정식을 풀어왔을 것이라고 생각합니다. 알고리즘의 절차를 정식으로 설명하기 전에, 간단히 두 개의 미지수 \(x\)와 \(y\)로 이루어진 예제 연립방정식의 풀이를 진행해보겠습니다.

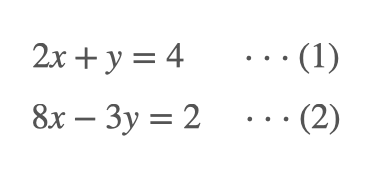
아마 대부분의 독자는 우선 (1)번 등식의 양변에 4를 곱한뒤, (2)번식에서 (1)번식을 빼줌으로써 (2)번식의 \(x\)항을 제거하였을 것입니다. 이 경우 아래와 같은 새로운 연립방정식을 만들 수 있습니다.

하나의 식에서 다른 식을 더하거나 빼는 과정이 전체 연립방정식의 해에 영향을 주지 않는다는 것을 자연스럽게 이해하고 있었기에 위의 단계를 수행할 수 있었습니다. 이제 (2)번식은 미지수가 1개인 일차방정식이 되었음으로 \(y\)의 값이 \(2\)가 되어야 함을 쉽게 알 수 있습니다. 최종적으로 해당 값을 (1)번식에 대입하여 \(x\)의 값이 1이 되어야 하는 것까지 확인할 수 있습니다.

위의 풀이는 중학교 교육과정 중 "가감법을 이용한 연립방정식의 풀이"를 이용한 것으로 실제 가우스 소거법에서 사용하는 아이디어와 동일합니다.

---

2. 가우스 소거법 : [m x n] 행렬

위의 \([2 \times 2]\) 예시에서의 아이디어를 그대로 일반적인 \([m \times n]\) 크기의 행렬에 적용할 수 있습니다. 여기에서 피벗(pivot)이라는 새로운 개념을 소개하겠습니다. 피벗이란 가우스 소거법을 이용하여 변환된 최종 연립방정식에서 각 방정식의 첫번째 0이 아닌 계수를 의미하는 것으로, 모든 \([m \times n]\) 행렬은 최대 \(min(m, n)\)개의 pivot을 가질 수 있습니다.

일반적으로 \([m \times n]\) 크기의 행렬에서 첫번째 피벗은 첫번째 방정식의 첫번째 항의 계수가 됩니다. 위의 \([2 \times 2]\) 예시에서 \(x\)의 계수인 2가 이에 해당합니다. 이후 행간 연산(Row operation)을 통해 두번째~마지막 방정식의 \(x\)항을 모두 소거합니다. 이때 \(i\)번째 방정식의 \(x\)항을 소거하기 위해서는 \(i\)번째 방정식에서 첫번째 방정식의

$$ \frac{i번째 방정식의 첫번째 항의 계수}{첫번째 피벗}배$$

만큼을 빼주면 됩니다. 위의 \([2 \times 2]\) 예시에서는 \((2)\)번 방정식에서 \((1)\)번 방정식의 \(\frac{8}{2}\)배 만큼을 빼주는 과정이 이에 해당합니다. 이를 이용하여 \({2, 3, 4, ..., m}\)번째 방정식에 대해 첫번째 항의 소거를 진행합니다. 이후, 동일한 방법을 사용하여 \(k\)번째 방정식으로부터 \({k+1, k+2, ..., m}\)번째 방정식에 대해 소거를 상삼각행렬(Upper triangular matrix) 형태의 계수 행렬(Coefficient matrix)을 얻을때까지 계속하면 됩니다.

(예제 1) 아래의 연립방정식을 가우스 소거법을 이용하여 단순화하시오

[단계 1] : 2, 3번째 방정식의 x항을 소거

[단계 2] : 3번째 방정식의 y항을 소거

[단계 3] : Upper triangular system으로 정리

Ux' = b' 형태로 재표현 (U는 상삼각행렬)

많은 교보재에서 최종적인 변환형태에서의 삼각행렬을 Upper triangular의 앞글자를 따서 \(U\)로 지칭하는 경우를 많이 살펴볼 수 있습니다. 이 블로그의 포스트에서도 앞으로 해당 행렬은 \(U\)로 표기합니다.

---

3. Back Substitution

가우스 소거법을 이용하여 연립방정식을 단순화한뒤, 실제 \(x\)(벡터)의 값을 구하기 위해서는 Back substitution이라는 기법을 사용합니다. 이 기법에 대해서 소개를 따로 드리지 않았더라도, 소거가 완료된 \(Ux'=b'\)에서 아마 대부분 자연스럽게 이 방식을 사용할것이라고 생각합니다.

우선 위의 [예제 1]에서 자유도가 0인 마지막 방정식(\(3z = 9\))을 통해 \(z\)의 값을 알아낼 수 있습니다. 알아낸 \(z\)의 값을 두번째 방정식에 대입하여 또다시 자유도가 0인 방정식에서 \(y\)의 값을 알아내고, 동일한 방식으로 \(x\)(스칼라)의 값까지 모두 알아낼 수 있습니다. 이처럼 아래에서 위의 방향으로 하나씩 변수의 값을 알아내고 이를 다음 방정식에 대입함으로써 그 다음 변수의 값을 알아내는 과정을 Back substitution이라고 부릅니다(이에 대응하여 가우스 소거법을 Forward Elimination 이라고 부르기도 함).

예시로 위 [예제 1]의 연립방정식의 해는 아래와 같이 구할 수 있습니다.

x=1, y=2, z=3

---

4. 가우스 소거법의 실패 Case

불행히도(?) 가우스 소거법을 이용하여 모든 \([m \times n]\) 행렬이 성공적으로 Upper triangular system으로 변환되는 것은 아닙니다. 여기에서 말하는 성공이란 \(Ax=b\)에서 해가 유일하게 결정되기 위한 필요조건으로써, 피벗의 개수가 \(min(m, n)\)과 동일한 경우를 지칭합니다. 위의 [예제 1]의 경우 피벗의 개수가 3개로 성공적인 Case를 보여주고 있습니다. 지금부터는 실패할 수 있는 Case를 살펴보겠습니다.

(예제 2) 아래의 연립방정식을 가우스 소거법을 이용하여 단순화하시오

[단계 1] : 2, 3번째 방정식의 x항을 소거

x항을 소거하는 과정에서 2, 3번째 방정식의 y항이 사라짐

[단계 2] : 3번째 방정식의 y항을 소거([단계1]에서 이미 완료)

[단계 3] : 3번째 방정식의 z항을 소거([2,3]번째 원소가 pivot이 되므로)

[단계 4] : Upper triangular system으로 정리

위의 예제는 최종적으로 생성된 삼각행렬에서 2개의 피벗만이 존재하는 경우로 가우스 소거법의 실패 Case에 속합니다. 실패 Case라는 것은 유일해가 존재할 일은 절대 없다는 것을 우리에게 알려주는 것입니다. 최종적으로 정리된 연립방정식을 얼핏 보았을 때, 해를 구할 수 있을 것 같지만 \(z\)의 값이 1이라는 것만 결정할수 있을 뿐, 연립방정식을 만족할 수 있는 \(x\)와 \(y\)의 조합은 무수히 많습니다. 첫번째 방정식의 자유도가 1이기 때문입니다.

$$x + 2y - 1 = 2$$

반대로 해가 아예 존재하지 않는 경우도 있습니다. 위의 [예제 2]에서 최초 3번째 방정식의 \(z\)항 계수를 \(-1\)에서 \(1\)로 변경한 뒤 가우스 소거법을 통해 \(Ux'=b'\)의 형태로 재표현해보겠습니다.

(예제 3) 아래의 연립방정식을 가우스 소거법을 이용하여 단순화하시오

[단계 1] : 2, 3번째 방정식의 x항을 소거

[단계 2] : 3번째 방정식의 y항을 소거([단계1]에서 이미 완료)

[단계 3] : 3번째 방정식의 z항을 소거([2,3]번째 원소가 pivot이 되므로)

[단계 4] : Upper triangular system으로 정리

최종적으로 정리된 연립방정식에서 \(0 = -2\)라는 모순적인 등식이 도출되는 것을 확인할 수 있습니다. 이는 해당 연립방정식의 해가 존재하지 않는다는 것을 의미합니다. 0벡터와 내적(inner-product)을 수행하였을 때 0이 아닌 값을 내뱉는 것은 불가능하기 때문입니다.

---

마치며

가우스 소거법은 매우 간단하고 직관적인 방법을 통해 연립방정식의 해를 가장 쉽게 계산가능한 형태로 변환해주는 알고리즘입니다. 이를 통해 생성된 \(Ux'=b'\)의 형태에서 피벗의 개수를 세어봄으로써 연립방정식의 해에 대한 정보를 얻을 수 있었습니다.

가우스 소거법을 이용하여 도출된 새로운 \(Ux'=b'\)로부터 연립방정식의 해와의 관계는 아래와 같이 정리할 수 있습니다.

※ 이 글은 Gilbert Strang 교수님의 MIT OCW 강의와 저서 「Introduction to Libear Algebra」를 참고하여 정리한 자료임을 밝힙니다. 여유가 되신다면 아래 첨부한 교수님의 강의를 들어보시는 것도 권장합니다.

---

[링크 1.] 가우스 소거법(Gaussian Elimination)에 대한 Gilbert Strang 교수님의 MIT 강의

https://www.youtube.com/watch?v=QVKj3LADCnA&list=PL221E2BBF13BECF6C&index=7 

MIT OCW 18.06 [2. Elimination with Matrices]

---

[링크 2.] Gilbert Strang 교수님의 선형대수 Course(18.06)에 대한 MIT OCW 홈페이지

https://ocw.mit.edu/courses/18-06-linear-algebra-spring-2010/

Linear Algebra | Mathematics | MIT OpenCourseWare